Depth-first search (maze generation algorithm)

Posted on October 10, 2021

Graphs

In general, a graph is a way to model pairwise relationships between things. The things are represented by nodes (or vertices; I will use both interchangeably) in the graph, and the relationships are represented by the lines joining them, called edges. You can probably tell by how general that definition is, that graphs have a ton of different applications in a lot of different problems. Suffice it to say, they are quite useful to model some very interesting problems. We will take a look at one of these problems which happens to be quite fun, and can lead to cool looking results - the problem of generating and solving random mazes.

Grids as graphs

We will make our maze from a 2-D grid, and the first thing we need to do is model the grid as a graph. This model is just a way to think about the problem in a systematic way. Take a look at the grid below — its a 2-D grid, but it doesn’t have to be 2-D, it can be an \(n\)-D grid. This grid (and indeed, any \(n\)-D grid) can be represented as a graph. Each cell of the grid can be a vertex of the graph while the edges can represent the spatial relationships between the vertices. For example, a cell in the interior of the grid (i.e. a cell that is not at the boundary) is represented by a vertex in the graph, and all of its neighbours will be represented by the vertices connected to its vertex.

The above two representations are equivalent — each cell is a node and neighboring relationships are indicated by edges

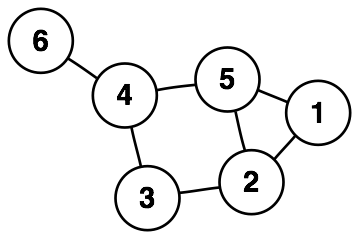
Graph traversal

A graph traversal is the process of visiting every node of a graph, and the algorithms that perform this are called graph traversal algorithms. If done creatively, these algorithms can help generate and solve random mazes — we will see how below. If you didn’t see it already, I have an example of a maze generation algorithm running under the title on the homepage, click my name at the top of this page to see what’s in store. I will also talk about the code used for that animation in this post.

Depth-first search

The Depth-First Search (DFS) algorithm is one way of traversing a graph. As the name suggests, this algorithm traverses the graph in a way that first explores the graph by going deep into it, then backtracking before finding another path to go deep into, until the whole graph has been explored. If you sit down and try to come up with an algorithm (a set of instructions) for exploring all the nodes of a graph, you will likely come up with this one. In words, the DFS algorithm does the following:

Start from a “root” node.
Keep track of the explored nodes at every point in time.
Pick one “child” node of the “root” node at random, and go to it.
Repeat this process until you can’t no more.
Backtrack to a node with unexplored “child” nodes.
Repeat 3-5 until you can’t no more.

After performing this, you will have explored every node in the graph. Note that the algorithm isn’t actually a 6-step process. In fact, this version is expanded for clarity, you could definitely make that list shorter with better wording. As with almost everything, DFS is much easier to understand if you try to implement it. Maze generation is an interesting and entertaining way to learn about graph search algorithms like DFS.

Maze generation using DFS

Think about the game of snake from those really old Nokia phones. I’m not going to push this analogy too hard, but imagine that snake randomly moving on this grid. If we simply remove the walls between the explored cells (i.e. the path explored by the snake), it will carve out a path in the maze. In the process of backtracking and exploring other paths, the snake will carve out many other paths (and dead ends) in the maze, which is exactly what we want!